Question

The center of the circle below is at P. If the radius is 8 cm. and the length of arc AB is 7 cm., find the central angle < APB to the nearest whole degree.

Answer 1

GIVEN:

We are given a circle with center P, a radius of length 8cm and an arc AB with length 7cm.

Required;

To find the angle measure of the central angle APB of the circle given.

Step-by-step solution;

To find the central angle of the circle given the above information, we begin by taking note of the formula for the length of an arc, and that is;

`\begin{gathered} Length\text{ }of\text{ }an\text{ }arc: \\ \\ L=(\theta)/(360)*2\pi r \end{gathered}`

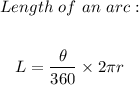
The variables given here are;

`\begin{gathered} r=8cm \\ \\ L=7cm \\ \\ \theta=? \end{gathered}`

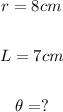
Now we will substitute the known values as follows;

`\begin{gathered} 7=(\theta)/(360)*2*3.14*8 \\ \\ 7=(\theta*2*3.14*8)/(360) \\ \\ 7=(50.24*\theta)/(360) \end{gathered}`

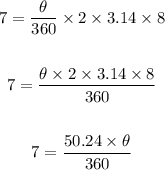
Next, we cross multiply;

`\begin{gathered} (7*360)/(50.24)=\theta \\ \\ 50.1592356688=\theta \end{gathered}`

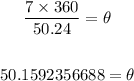
Rounded to the nearest degree, we now have;

ANSWER:

`\theta=50\degree`

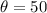
Option A is the correct answer.