Question

Which ordered pairs are solutions to the inequality 4x+y>−6?

Select each correct answer.



(2, 0)

(−3, 6)

(4, −20)

(0, −9)

(−1, −1)

Answer 1

The ordered pairs that are solutions to the inequality 4x+y>-6 are (2, 0), (4, -20), and (-1, -1) as they satisfy the condition when substituted into the inequality.

Step-by-step explanation:

To determine which ordered pairs are solutions to the inequality 4x+y>-6, we need to plug the x and y values from each ordered pair into the inequality.

• For the pair (2, 0), we substitute x = 2 and y = 0 into the inequality: 4(2) + 0 > -6, which simplifies to 8 > -6. This is true, so (2, 0) is a solution.
• For the pair (-3, 6), we substitute x = -3 and y = 6: 4(-3) + 6 > -6, which simplifies to -12 + 6 > -6. This gives -6 > -6, which is not true, so (-3, 6) is not a solution.
• For the pair (4, -20), we substitute x = 4 and y = -20: 4(4) - 20 > -6, which simplifies to 16 - 20 > -6. This gives -4 > -6, which is true, so (4, -20) is a solution.
• For the pair (0, -9), we substitute x = 0 and y = -9: 4(0) - 9 > -6, which simplifies to -9 > -6. This is not true, so (0, -9) is not a solution.
• For the pair (-1, -1), we substitute x = -1 and y = -1: 4(-1) - 1 > -6, which simplifies to -4 - 1 > -6. This gives -5 > -6, which is true, so (-1, -1) is a solution.

The correct solutions to the inequality are the ordered pairs (2, 0), (4, -20), and (-1, -1).

Answer 2

(2,0) , (4,-20) and (-1,-1)

Step-by-step explanation:

`4x+y>-6`

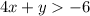
WE need to select an ordered pair that is solution to our inequality

Lets check with each option

(2,0) , plug in 2 for x and 0 for y

`4x+y>-6`

`4(2)+0>-6`

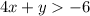
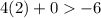
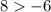`8>-6` True

(−3, 6), plug in -3 for x and 6 for y

`4x+y>-6`

`4(-3)+6>-6`

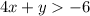
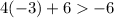
`-6>-6` False

(4, −20) , plug in 4 for x and -20 for y

`4x+y>-6`

`4(4)-20>-6`

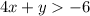
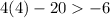
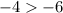`-4>-6` True

(0, −9) , plug in 0 for x and -9 for y

`4x+y>-6`

`4(0)-9>-6`

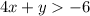
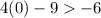
`-9>-6` False

(-1, −1) , plug in -1 for x and -1 for y

`4x+y>-6`

`4(-1)-1>-6`

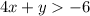
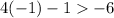
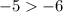`-5>-6` True