Answer:
103 mg.
Explanation:
We have been given that the decay of 230 mg of an isotope is described by the function
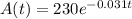 , where t is time in years.
, where t is time in years.
To find the amount left after 26 years, we will substitute
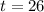 in our given function as:
in our given function as:
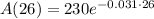
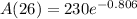
Using exponent property
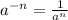 , we will get:
, we will get:

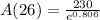
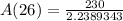
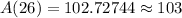
Therefore, 103 mg of isotope will be left after 26 years.