Question

(CO 3) Ten rugby balls are randomly selected from the production line to see if their shape is correct. Over time, the company has found that 92.4% of all their rugby balls have the correct shape. If exactly 7 of the 10 have the right shape, should the company stop the production line?

Answer 1

GIVEN:

We are told that ten rugby balls are randomly selected from the production line to see if their shape is correct.

Over time, the company has found that 92.4% of all their rugby balls have the correct shape.

Required;

If exactly 7 of the 10 have the right shape, should the company stop the production line?

Step-by-step solution;

The sample for this experiment size is 10, the number of successes is 7 and the probability is 0.924.

In order to solve this problem we shall apply the binomial distribution formula which;

`P(x)=(_x^(_n))P^x(1-P)^(n-x)`

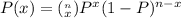
Now we substitute the given values and we'll have;

`\begin{gathered} P(x=7)=(_7^(10))*(0.924)^7*(1-0.924)^(10-7) \\ \\ P(x=7)=120*0.575047604381*0.000438976 \\ \\ P(x=7)=0.0302918516617 \\ \\ P(x=7)\approx0.0303 \end{gathered}`

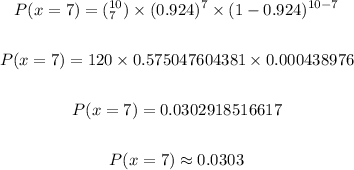
Notice that this is less than 0.05, that is;

`0.0303<0.05`

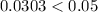
This probability is unsual. Hence,

ANSWER: Yes the company should stop the production line since the probabilty of 7 balls having the correct shape is unusual.