GIVEN:
We are told that ten rugby balls are randomly selected from the production line to see if their shape is correct.
Over time, the company has found that 92.4% of all their rugby balls have the correct shape.
Required;
If exactly 7 of the 10 have the right shape, should the company stop the production line?
Step-by-step solution;
The sample for this experiment size is 10, the number of successes is 7 and the probability is 0.924.
In order to solve this problem we shall apply the binomial distribution formula which;
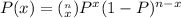
Now we substitute the given values and we'll have;
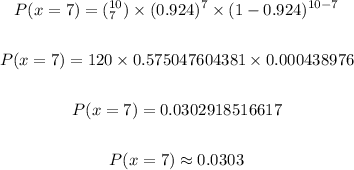
Notice that this is less than 0.05, that is;
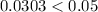
This probability is unsual. Hence,
ANSWER: Yes the company should stop the production line since the probabilty of 7 balls having the correct shape is unusual.