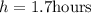Question

Finding the time given an exponential function with base e that models a real world situation

Answer 1

The time needed before the patient is to be injected again is;

`h=1.7\text{ hours}`

Step-by-step explanation:

Given that the function that can model the exponential relationship between time (h) and the milligram of a drug in a patient's bloodstream D(h) is;

`D(h)=50e^(-0.25h)`

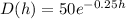
we want to calculate the time in hours before a patient is to be injected again when;

`D(h)=33`

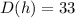
Substituting in the given function, we have;

`\begin{gathered} D(h)=50e^(-0.25h) \\ 33=50e^(-0.25h) \end{gathered}`

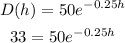
taking the natural logarithm of the function;

`\begin{gathered} 33=50e^(-0.25h) \\ ln33=ln50-0.25h \\ 0.25h=ln50-ln33 \\ h=(ln50-ln33)/(0.25) \\ h=1.66 \\ h=1.7\text{ hours} \end{gathered}`

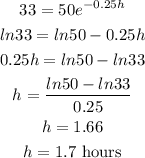
Therefore, the time needed before the patient is to be injected again is;

`h=1.7\text{hours}`