Answer:
The time needed before the patient is to be injected again is;
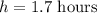
Step-by-step explanation:
Given that the function that can model the exponential relationship between time (h) and the milligram of a drug in a patient's bloodstream D(h) is;
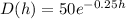
we want to calculate the time in hours before a patient is to be injected again when;
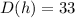
Substituting in the given function, we have;
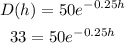
taking the natural logarithm of the function;
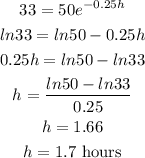
Therefore, the time needed before the patient is to be injected again is;
