Answer:
Triangle ABC translate 1 unit left and 1 units down to get the triangle A'B'C'. The rule of translation is
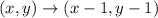
Explanation:
Given information: In triangle ABC, A(-5,1), B(-2,7), C(0,1). In triangle A'B'C', A'(-6,0), B'(-3,6), C'(-1,0).
Let the rule of translation be

where, a is horizontal shift and b is vertical shift.
If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.
If b<0, then the graph shifts b units up and if b>0, then the graph shifts b units down.
It is given that A(-5,1) and A'(-6,0).
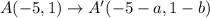
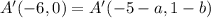
On comparing both sides, we get

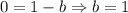
The value of a is 1 and value of b is 1. So, the rule of translation is
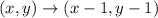
Therefore the triangle ABC translate 1 unit left and 1 units down to get the triangle A'B'C'.