2 Answers

Ben Vitale · Answer 1 · 2018-12-10T14:27:37+0000

Answer:

The correct option is C.

Explanation:

From the given figure it is clear that the vertices of the parallelogram are (0,0), (0,-6), (4,-8) and (4,-2).

If a figure rotated 180° about (a,b), then

$(x,y)\rightarrow (2a-x,2b-y)$

If the figure rotated 180° about (2,-4), then

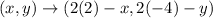
$(x,y)\rightarrow (2(2)-x,2(-4)-y)$

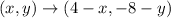
$(x,y)\rightarrow (4-x,-8-y)$

So, the vertices of image after rotated 180° about (2,-4) are

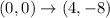
$(0,0)\rightarrow (4,-8)$

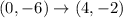
$(0,-6)\rightarrow (4,-2)$

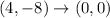
$(4,-8)\rightarrow (0,0)$

$(4,-2)\rightarrow (0,-6)$

The vertices of image are same as vertices of preimage. So, 180° rotation about (2,-4) maps the figure onto itself.

Therefore the correct option is C.

Please log in or register to add a comment.