Completing the Frequency Table
We are asked to create a frequency table. We will create the table.
We know that we will have 205 dancers in total, so this can go in the bottom right hand corner.
Then, we need to find out how many in total were trained in tap and ballet. We are given the value of 72, so this goes under "Trained in Tap" and meets with "Trained in ballet."
Then, we are told that 43 train in ballet, but not in tap. Therefore, we will place 43 under "Trained in ballet" but line it up with "Not trained in tap."
Finally, we have that 62 dancers were not trained in either tap nor ballet, so 62 is placed in the cell that lines up "Not trained in tap" and "Not trained in ballet."
This gives us this frequency table:
Then, we need to perform some math to find out how to fill the cells. Let's find the total number of individuals trained in tap column.
We know that 72 are trained in tap, and that 205 is the total for the entire frequency. 105 are not trained in tap, so we can subtract 105 from 205 to get 100. That means the total for the Trained in tap column becomes 100.
Then we have to find how many are not trained in ballet but are trained in tap. This means that we need to subtract 72 from 100. This gives us 28, which means 28 dancers are not trained in ballet but are trained in tap.
Finally, we can find the total dancers not trained in ballet by adding 28 and 62, which gives us 90.
This gives us a final frequency table:
Finding Part A
Now, we need to find the percent of dancers that were not trained in either discipline. This means that we need to use the value of 62 dancers. We were told that 62 dancers were not trained in either discipline. Therefore, we know that we have 205 dancers in total, which means we will divide 62 by 205.
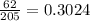
Then, we need to multiply this decimal by 100% to find the percentage of dancers not trained in either discipline.
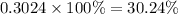
Therefore, 30.24% of dancers were not trained in either discipline.
Finding Part BPart B asks us to find what percent of tap dancers were also trained in ballet. Using our frequency table, we can see that 72 dancers were trained in both tap and in ballet. Therefore, we also know that 100 dancers were trained in tap. If 72 of those dancers were also trained in ballet, we can divide 72 by 100 and find the percentage using the same steps as above.

Then, we multiply the decimal by 100%.

Therefore, 72% of dancers that were trained in tap dance were also trained in ballet.