Answer:
Part a)
y = 30.625 m
Part b)
v = 24.5 m/s
Step-by-step explanation:
Part a)
As we know that brick will hit the floor after t = 2.50 s
so here we will have

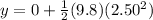

Part b)
velocity of the brick just before it will strike the ground is given as
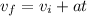

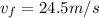
Part c)