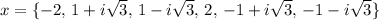There are two possible solutions:
1)
When we know that:
![\sqrt[n]{z}=\sqrt[n]\Big(\cos(\phi+2k\pi)/(n)+i\sin(\phi+2k\pi)/(n)\Big)\qquad\text{for}\quad k=0,1,\ldots,n-1](https://img.qammunity.org/2018/formulas/mathematics/college/djms7n7ksvilso2o58g27is04dynh6evpv.png)
when
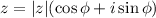
then:
![x^6=64\quad|\sqrt[6]{(\ldots)}\\\\x=\sqrt[6]{64}](https://img.qammunity.org/2018/formulas/mathematics/college/yarpcm7aum71xu2yhcrkikfzvwb4l68f3h.png)
For
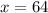
we have:
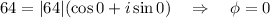
and:
![\sqrt[6]{64}=\sqrt[6]{64}\Big(\cos(0+2k\pi)/(6)+i\sin(0+2k\pi)/(6)\Big)\qquad\text{for}\quad k=0,1,\ldots,5\\\\\\ \sqrt[6]{64}=2\Big(\cos(k\pi)/(3)+i\sin(k\pi)/(3)\Big)\qquad\text{for}\quad k=0,1,\ldots,5](https://img.qammunity.org/2018/formulas/mathematics/college/obe26hd8hz2mbrsp0wlhyhj3mk47j0wip4.png)
k = 0
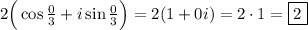
k = 1
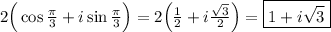
k = 2
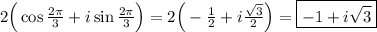
k = 3
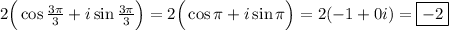
k = 4
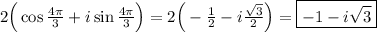
k = 5

So the answer is:
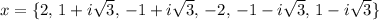
2)
We don't know method (1). If so, we could use following identities:
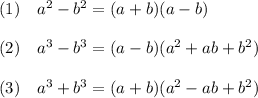
There will be:
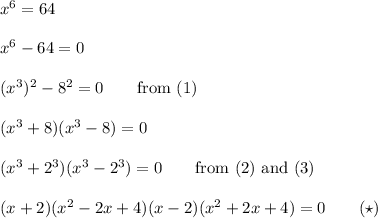
Now, we complete the square for:
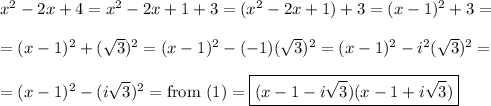
and for:
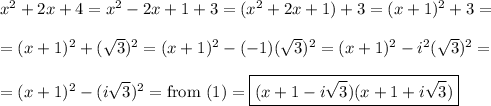
When we return to
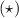
:
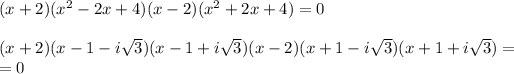
And we have answer: