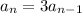Question

State whether each sequence is arithmetic or geometric, and then find the explicit and recursive formulas for each sequence.

Part1. 10,15,20,25,30.. Step 1.State whether this sequence is arithmetic or geometric and find the explicit formula. show your work. Step 2. find the recursive formula. Show your work.
Part 2. 2,6,18,54,162.. Step 1. State whether this sequence is arithmetic or geometric and find the explicit formula. show your work. Step 2.find the recursive formula. Show your work

Answer 1

First let's talk about how to tell if a sequence is arithmetic or geometric. If a sequence is arithmetic, that means that every step between terms is either adding or subtracting in a pattern. Let's look at Part 1, which is an example of this:

Part 1: 10, 15, 20, 25, 30, ... Look at the difference between the first term and the second term: it's increased by 5. Now look at the difference between all following terms and you'll notice that this pattern is repeated. Then our recursive formula would be:

`a_(n)=a_(n-1)+5`

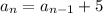
Now a geometric sequence, on the other hand, will have a common ratio between terms. This means that the second term divided by the first term will give you the same number as the fifth term divided by the fourth term. Let's look at Part 2:

Dividing the second term by the first term, we see that the ratio is 6/2=3. Now dividing any other two terms similarly, we can see that the ratio is still 3. Then our recursive formula is:

`a_n=3a_(n-1)`