Question

A trapezoid has an area of 20 cm2 and a height z cm. The lengths of the parallel sides are (2z + 3) cm and (6z – 1) cm. Find the height, z, of the trapezoid. In your final answer, include all of the formulas and calculations necessary.

Answer 1

check the picture below.


`\bf A=\cfrac{h(a+b)}{2}\quad \begin{cases} A=20\\ a=6z-1\\ b=2z+3\\ h=z \end{cases}\implies 20=\cfrac{z[(6z-1)~+~(2z+3)]}{2} \\\\\\ 20=\cfrac{z(8z+2)}{2}\implies 20=\cfrac{2z(4z+1)}{2}\implies 20=z(4z+1) \\\\\\ 20=4z^2+z\implies 0=4z^2+z-20`


`\bf \qquad \qquad \textit{quadratic formula}\\\\ \begin{array}{llccll} 0=&{{ 4}}z^2&{{ +1}}x&{{ -20}}\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array} \qquad \qquad z= \cfrac{ - {{ b}} \pm \sqrt { {{ b}}^2 -4{{ a}}{{ c}}}}{2{{ a}}} \\\\\\ z=\cfrac{-1\pm√(1+320)}{8}\implies z=\cfrac{-1\pm√(321)}{8}\implies z\approx \begin{cases} \boxed{2.1146}\\ -2.3646 \end{cases}`

since the height is just a length unit, it can't be -2.3646.

Answer 2

2.11 cm

Explanation:

As you can see in the picture I put the sides in the trapezoid. Now, let's use the area's formula:

A =
`((B+b)*h)/(2)`

where B is the Largest parallel side, b the smallest parallel side and h is the height.

Now,

20 =
`((6z-1+2z+3)*z)/(2)`

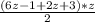
20 =
`((8z^(2)+2z)/(2)`

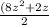
20 =
`4z^(2)+z`

`4z^(2)+z-20=0`

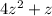
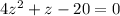
Then, we use the cuadratic formula z=
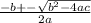`\frac{-b+-\sqrt{b^(2)-4ac} }{2a}` where a=4, b=1 and c=-20.

z=
`(-1+-√(1-4(4)(-20)) )/(8)`

z =
`(-1+-√(1+320) )/(8)`

z =
`(-1+-√(1+320) )/(8)`

z =
`(-1+-17.91)/(8)`

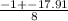
As we are searching lenght we choose the positive z value

z =
`(-1+17.91)/(8)`

z=
`(16.91)/(8)`

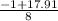
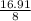
z = 2.11 cm.