Question

A balloon is released on top of a building. The graph shows the height of the balloon over time. What does the slope and y-intercept reveal about the situation?

Answer 1

C. The balloon starts at a height of 500 ft and rises at a rate of 150 ft.

Explanation:

We have been given a graph which represents the height of the balloon over time.

We can see from our graph that y-intercept, which represents the height of the balloon (in thousand feet) at time equals zero, is 0.5. To find the correct y-intercept we will multiply 0.5 by 1000 as height of the balloon is given in thousand feet.

`\text{y-intercept}=(0.5* 1000)\text{ feet}=500\text{ feet}`

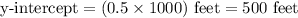
Therefore, y-intercept represents that the balloon starts at a height of 500 feet.

Now let us find slope of our given line using slope formula.

`\text{Slope}=(y_2-y_1)/(x_2-x_1)`

`y_2-y_1` is vertical change or rise.

`x_2-x_1` is horizontal change or run.

Upon substituting given values in above formula we will get,

`\text{Slope}=(3.5-0.5)/(20-0)`

`\text{Slope}=(3)/(20)`

`\text{Slope}=0.15`

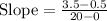
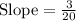
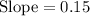
Now let us multiply 0.15 by 1000 as height of balloon is given in thousand feet.

`\text{Slope}=0.15* 1000=150`

Therefore, slope of our line is 150 which means that height of balloon is increasing 150 feet per second or balloon is rising at a rate of 150 feet per second.

Upon looking at our given options we can see that option C is the correct choice.

Answer 2

The slope is (change in y)/(change in x). Taking (0, 0.5) and (10, 2) since the x axis is horizontal and the y axis vertical, we get the slope to be (2-0.5)/(10-0)=
1.5/10=3/20=0.15. Since it's based off of 1000 feet, we multiply 0.15 by 1000 to get 150 as the rate of change for every x value. In addition, since we start at 0.5, 1000*0.5=500 and we therefore start at 500 ft. Using the information we have, we therefore have C as our answer