Question

The function f(t) = t2 + 6t − 20 represents a parabola.

Part A: Rewrite the function in vertex form by completing the square. Show your work.
Part B: Determine the vertex and indicate whether it is a maximum or a minimum on the graph. How do you know?
Part C: Determine the axis of symmetry for f(t)

Answer 1

For t²+6t-20=0 (to find the vertex, or rather the x intercepts), we can add 20 to both sides to get t²+6t=20. Since 6/2=3, we can square 3 to get 9. Adding 9 to both sides, we get t²+6t+9=20+9=29=(t+3)². Finding the square root of both sides, we get t+3=+-√(29). Subtracting 3 from both sides, we get t=+-√(29)-3=either √(29)-3 or -√(29)-3. We have -√(29)-3 due to that t can either be negative or positive. Finding the average of the two numbers, we have
(√(29)-3)+(-√(29)-3./2=-6/2=-3, which is our t value of our vertex and since it's t² and based around t, that is our axis of symmetry. To find the y value of the vertex, we simply plug -3 in for t to get 9+(6*-3)-20=9-18-20=-29, making our vertex (-3, -29)

Answer 2

PART A:

The function in vertex form by completing the square is:

`f(t)=(t+3)^2-29`

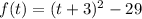
PART B:

The vertex is located at (-3,-29)

and the vertex is the minimum point of the graph.

PART C:

The axis of symmetry of f(t) is:

t= -3

Explanation:

The function f(t) is given by:

`f(t)=t^2+6t-20`

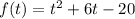
We know that the vertex form of a equation is given by:

`f(t)=a(t-h)^2+k`

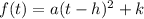
where a,h and k are real numbers.

and the vertex is located at (h,k)

The function is given by:

`f(t)=(t+3)^2-29`

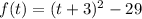
Hence, the vertex is given by:

(-3,-29)

Also, as the leading coefficient is positive.

Hence, the parabola is upward open parabola.

Hence, the vertex will be the minimum point of the graph.

Also, the axis of symmetry of a graph is given by:

t=h

Hence, here the axis of symmetry is: t= -3