Question

An important part of customer service responsibilities of a cable company relates to the speed with which trouble in service can be repaired. Historically, the data show that the likelihood is 0.75 that troubles in a residential service can be repaired on the same day. For the first 5 troubles reported on a given day, what is the probability that fewer than 2 troubles will be repaired on the same day?

Answer 1

The answer to your question is
D. .2373


Hope this helps

Answer 2

The probability that fewer than 2 troubles will be repaired on the same day is:

0.015576

Explanation:

We have to use the Binomial function is n=order to calculate the probability of r successes out of the n-events.

We know that the probability of r success out of the n-events is given by:

`P(X=r\ successes)=n_C_r\cdot p^r\cdot (1-p)^(n-r)`

where p is the probability of an success.

Here we have:

n=5 and r=0,1.

since we are asked to find the probability that fewer than 2 troubles will be repaired on the same day.

i.e we have to find:

`P(X<2)=P(X=0)+P(X=1)`

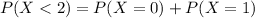
Also p=0.75 ( since, likelihood is 0.75 that troubles in a residential service can be repaired on the same day )

Hence,

`P(X=0)=5_C_0\cdot (0.75)^(0)\cdot (1-0.75)^(5-0)\\\\P(X=0)=1\cdot 1\cdot (0.25)^5\\\\P(X=0)=0.000976`

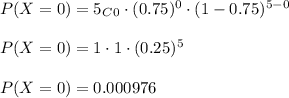
and

`P(X=1)=5_C_1\cdot (0.75)^(1)\cdot (0.25)^(5-1)\\\\P(X=1)=5\cdot (0.75)\cdot (0.25)^4\\\\P(X=1)=0.0146`

Hence,

`P(X<2)=0.000976+0.0146\\\\P(X<2)=0.015576`

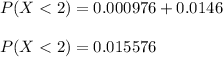
Hence, the probability that fewer than 2 troubles will be repaired on the same day is:

0.015576