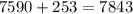Solution
- Before we begin solving, let us first know what the result of the original product is
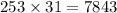
- Now, let us analyze what was done on both diagrams.
Diagram A:
- In this diagram, 253 was divided into 3 numbers and 31 was divided into two numbers.
- We can visualize this better if we wrote them in the product form as shown above:

- We can therefore see that the empty boxes simply represent the product of these numbers stated above.
- Thus, we can easily populate the boxes if we just perform the products associated with them.
- That is:
- Adding up all the numbers in all 6 squares, we have
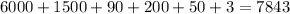
- This is the same result as the original product
Diagram B:
- For this diagram, we take a similar approach
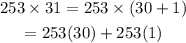
- Placing these products in their respective boxes, we have:
- Again, Adding up these numbers in the boxes we have: