Question

You may write negative infinity, positive infinity or all reals if you must use these as part of your answer. Separate numbers using commas and use the word nine if needed.

Answer 1

`\begin{gathered} a)D=(-3,infinity) \\ b)R=(-infinity,infinity) \\ c)x=-2 \\ d)y=1.58496 \\ e)x=-2\:Vertical\:Asympote,\:No\:Horizontal\:Asymptote \end{gathered}`

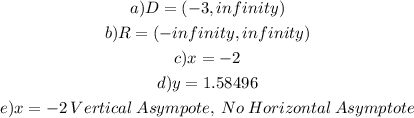
a) Let's find the Domain of that logarithmic function by finding the values that are undefined for this function, so we can do the following:

`\begin{gathered} f(x)=\log_2(x+3) \\ x+3>0 \\ x>-3 \\ D=(-3,\infty) \end{gathered}`

Note that the argument of a logarithm must be greater than 0.

b) Range

For the range, we can find the Range of this function by doing this:

`R=(-\infty,\infty)`

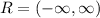
Since there are no discontinuities along with the function.

c) The x-intercept

We can plug into that y=0 and find the x-intercept

`\begin{gathered} \log_2(x+3)=0 \\ x+3=2^0 \\ x+3=1 \\ x=1-3 \\ x=-2 \end{gathered}`

d) What is the y-intercept

Similarly, we can plug into the function x=0

`\begin{gathered} y=\log_2\left(0+3\right)\: \\ y=\log_2\left(3\right)\: \\ y=1.58496 \end{gathered}`

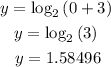
e) Asymptote

The asymptote is the line that demarks the points that the graph won't trespass:

`\begin{gathered} f(x)=\log_2(x+3) \\ \:f\left(x\right)\:=\:c\cdot \:log_a\left(x+h\right)+k \\ Vertical\:asymptote:x=-3 \\ No\:Horizontal\:asymptote \end{gathered}`

Note that the vertical asymptote is located at the value of h