Question

Simplify. −64x6y9−−−−−−−√3 assume all variables are nonnegative.

Answer 1

`-4x^2y^3`

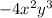
Explanation:

We have been given an expression
`\sqrt[3]{-64x^6y^9}`. We are asked to simplify our given expression.

Applying radical rule
`\sqrt[n]{-a}=-\sqrt[n]{a}`, when n is odd, we will get:

`-\sqrt[3]{64x^6y^9}`

We can rewrite terms of our given expression as:

`-\sqrt[3]{(4)^3(x^2)^3(y^3)^3}`

Using radical rule
`\sqrt[n]{a^n}=a`, we will get:

`-4x^2y^3`

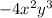
Therefore, simplified form of our given expression is
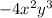`-4x^2y^3`.

Answer 2

In this item, I take it that we are to get the cube root of the given expression, -64x6y9. First, we look into the numerical coefficient, this is the product when -4 is multiplied to itself three times as shown below.

-64 = (-4)(-4)(-4)

Then,
x6 = x2 (x2) (x2)

and,
y9 = (y3)(y3)(y3)

If we take the cube root, we consider only one item per product. Thus, the answer is,

-4x²y³