Question

Suppose you have a U-Tube of radius 7.97 mm that is open on both ends. You pour some water in and then pour some unknown liquid on top of the water in the left hand tube. The system settles into the state shownIf the distances shown are d=7.8 cm and h=5.3 cm find the density of the unknown liquid.

Answer 1

404.58 kg/m³

Step-by-step explanation

The pressure on the water at the point where the unknown liquid and the water meet on the left-hand tube, PA, is,

`P_A=P_(atm)+\rho_(unknown)\cdot g\cdot\left(d+h\right)`

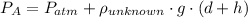
At the same time, the water exerts pressure on the unknown liquid which is,

`P_A=P_(atm)+\rho_(water)\cdot g\cdot h`

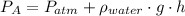
Where the unknown liquid and the water meet, the pressure is the same from both ends, so,

`P_(atm)+\rho_(unknown)\cdot g\cdot\left(d+h\right)=P_(atm)+\rho_(water)\cdot g\cdot h`

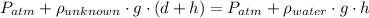
Atmospheric pressure cancels out,

`\rho_(unknown)g\mleft(d+h\mright)=\rho_(water)gh`

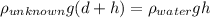
Also, the acceleration due to gravity cancels out,

`\rho_(unknown)\mleft(d+h\mright)=\rho_(water)h`

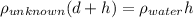
Solving for the density of the unknown liquid,

`\rho_(unknown)=(\rho_(water)h)/(\left(d+h\right))`

The density of pure water is 1000 kg/m³, h = 5.3 cm, and d = 7.8 cm. Replace with the known values and solve,

`\rho_(unknown)=(1000kg/m^3\cdot5.3cm)/((7.8+5.3)cm)\approx404.58kg/m^3`

Hence, the density of the unknown liquid is about 404.58 kg/m³, rounded to the nearest hundredth.