Checking for each option
Option A:
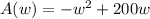
Substitute w = 10 and check if we'd get 900 as the answer
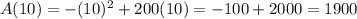
Option B:

Substitute w = 10 and check if we'd get 900 as the answer
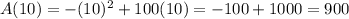
Option C:
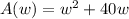
Substitute w = 10 and check if we'd get 900 as the answer

Option D:
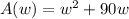
Substitue w = 10 and check if we'd get 900 as the answer
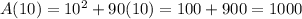
Answer: Option B