Question

Vanessa uses the expressions (3x2 + 5x + 10) and (x2 – 3x – 1) to represent the length and width of her patio. Which expression represents the area (lw) of Vanessa’s patio?

Answer 1

To find the answer to this, you have multiply both expressions by each other. To do this, you have to multiply each term in the first expression by each term in the second expressions. This yields the following: 3x^4-9x^3-3x^2+5x^3-15x^2-5x+10x^2-30x-10. Combing like terms and simplifying gives the final expression: 3x^4 - 4x^3 - 8x^2 - 35x - 10

Answer 2

`3x^(4)-4x^(3)-8x^(2)-35x-10`

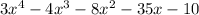
Explanation:

We have been given that Vanessa uses the expressions
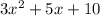`3x^2+5x+10` and
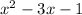`x^2-3x-1` to represent the length and width of her patio.

To find the expression that represents the area of Vanessa's patio we will multiply the length of patio by width of patio as:

`(3x^2+5x+10)*(x^2-3x-1)`

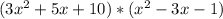
Upon using distributive property
`a(b+c)=a*b+a*c` we will get,

`(3x^2*x^2)+(3x^2*-3x)+(3x^2*-1)+(5x*x^2)+(5x*-3x)+(5x*-1)+(10x^2)+(10*-3x)+(10*-1)`

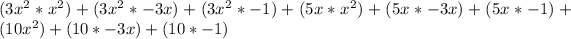
Using exponent property
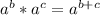`a^b*a^c=a^(b+c)` we will get,

`(3x^(2+2))+(-9x^(2+1))+(-3x^2)+(5x^(1+2))+(-15x^(1+1))+(-5x)+(10x^2)+(-30x)+(-10)`

`(3x^(4))+(-9x^(3))+(-3x^2)+(5x^(3))+(-15x^(2))+(-5x)+(10x^2)+(-30x)+(-10)`

`3x^(4)-9x^(3)-3x^2+5x^(3)-15x^(2)-5x+10x^2-30x-10`

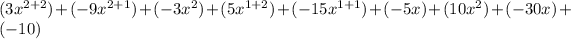
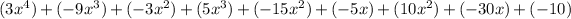
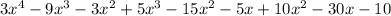
Now let us combine like terms.

`3x^(4)-9x^(3)+5x^(3)-3x^2-15x^(2)+10x^2-5x-30x-10`

`3x^(4)-4x^(3)-8x^(2)-35x-10`

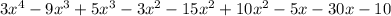
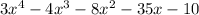
Therefore, the expression
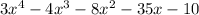`3x^(4)-4x^(3)-8x^(2)-35x-10` represents the area of Vanessa's patio.