Question

Given f(x)=6x^4, find f^-1(x). Then state whether f^-1(x) is a function.

Answer 1

The answer is C: y= +or-(x/6)^1/4 is a function

Explanation:

on edge :)

Answer 2

`f^(-1)(x)=((x)/(6))^{(1)/(4)}`

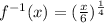
This is a function for [0,∞).

Explanation:

The given function is

`f(x)=6x^4`

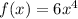
We need to find the
`f^(-1)(x)`.

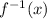Step 1: Replace f(x) be y.

`y=6x^4`

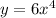
Step 2: Interchange x and y.

`x=6y^4`

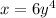
Step 3: Isolate variable y.

`(x)/(6)=y^4`

`((x)/(6))^{(1)/(4)}=y`

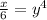
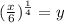
Step 4: Interchange the sides.

`y=((x)/(6))^{(1)/(4)}`

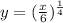
Step 5: Replace y by
`f^(-1)(x)`.

`f^(-1)(x)=((x)/(6))^{(1)/(4)}`

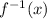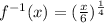
Therefore,
`f^(-1)(x)=((x)/(6))^{(1)/(4)}`.

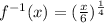This function is is defined for all positive values of x.

The inverse of function
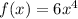`f(x)=6x^4` is a function for [0,∞).