Question

A swimming pool, 10.0 m by 4.0 m, is filled with water to a depth of 3.0 m at a temperature of 20.2°c. if the energy needed to raise the temperature of the water to 29.7°c is obtained from the combustion of methane (ch4), what volume of methane, measured at stp, must be burned? ∆hcombustion for ch4 = -891 kj/mol

Answer 1

You need to find the mass of water in the pool.
Find the volume (10 x 4 x 3) = 120 m3

Water has a density of 1000g/m3,so 120 m3 = 120 x 1000 = 120 000 kg

[delta]H = 4.187 x 120 000 x 3.4 (and the units will be kJ)

You then use the heat of combustion knowing that each mole of methane releases 891 kJ of heat so if you divide 891 into the previous answer, you will get the number of moles of CH4

Answer 2

119.69 kilo liter volume of methane measured at STP, must be burned.

Step-by-step explanation:

Length of the pool= 10.0 m

Breadth of the pool = 4.0 m

Height upto which the pool will be filled= 3.0 m

Volume of the water in the pool = volume of the pool :

= 10.0 m × 4.0 m × 3.0 m =
`120.0 m^3`

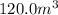
Density water =
`997 kg/m^3`

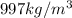
Mass of the water(m) =
`Density * volume =997 kg/m^3* 120 m^3=119,640 kg`

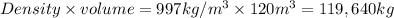
Energy required to raise the temperature = Q

Mass of the water = m = 119,640 kg =
`119,640* 1,000 g=119,640,000 g`

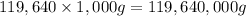
Specific heat of water ,c= 4.186 J/g °C

Change in temperature,
`\Delta T=29.7^oC-20.2^oC=9.5 ^oC`

`Q=mc\Delta T`

`Q=119,640,000 g* 4.186J/g ^oC* 9.5 ^oC`

`Q = 476,113.36* 10^4J=476,1133.6 kJ`

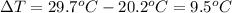
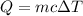
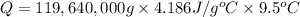
Heat required to raised the temperature is 476,1133.6 kJ.

Heat evolved when 1 mol of methane = -891 Kj

Number of moles of methane giving (- 476,1133.6) kJ of heat:

`(-476,1133.6 kJ.)/(-891)=5,343.58 mol`

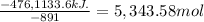
At STP, 1 mol occupies = 22.4 L

Then 5,343.58 mol will occupy :
`22.4* 5,343.58 L=119,696.19 l=119.69 kilo liter`

119.69 kilo liter volume of methane measured at STP, must be burned.