Question

Select the equation whose graph has a y-intercept with a positive y-coordinate. o y = 5x²-3x - 5 O y = x2 - 10x O y = x2 +3x-2 y = (x + 1)(x + 2)

Answer 1

The y-intercept of any function is the point where it intersects with the y-axis. At this point the x-coordinate is always zero.

To determine which equations have a positive y-intercept you have to determine the corresponding value for each one of them.

As mentioned above, the x-coordinate of the y-intercept is always zero, so to determine the y-coordinate of the point you have to replace each equation with x=0 and calculate the value of y:

First equation

`\begin{gathered} y=5x^2-3x-5 \\ y=5(0)^2-3\cdot0-5 \\ y=-5 \end{gathered}`

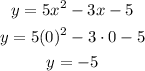
The y-intercept of this equation is (0,-5) and the y-coordinate is negative.

Second equation

`\begin{gathered} y=x^2-10x \\ y=0^2-10\cdot0 \\ y=0 \end{gathered}`

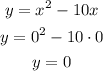
The y-intercept of this equation is the origin (0,0), zero is neither positive nor negative, so you can't say that the y-coordinate of the y-intercept of this equation is positive.

Third equation

`\begin{gathered} y=x^2+3x-2 \\ y=0^2+3\cdot0-2 \\ y=-2 \end{gathered}`

The y-intercept of this function is (0,-2) and its y-coordinate is -2 which is not positive.

Fourth equation

To determine the y-intercept of this equation first you have to solve the square of the binomial. For this you have to distribute the multiplication, which means, to multiply each term on the first parentheses by each term on the second parentheses:

`\begin{gathered} y=(x+1)(x+2) \\ y=x\cdot x+x\cdot2+1\cdot x+1\cdot2 \\ y=x^2+2x+x+2 \end{gathered}`

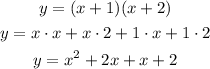
And simplify the like terms to determine the quadratic expression

`y=x^2+3x+2`

Now we can replace the expression with x=0 to determine the y-coordinate of the y-intercept

`\begin{gathered} y=0^2+3\cdot0+2 \\ y=2 \end{gathered}`

The y-intercept of this equation is (0,2) and has a positive y-coordinate.

So the only equation whose graph has a y-intercept with a positive y-coordinate is

y=(x+1)(x+2)