Question

Find the four real zeros of the polynomial. f(x) = x4 + 6x3 - 3x2 -52x - 60

A. 2, -2, -5, -3
B. -2, -2, -5, 3
C. -2, -2, 5, 3
D. 2, -2, -5, 3

Answer 1

The function is


`f(x)=x^4+6x^3-3x^2-52x-60`

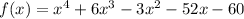
The "zeros" of a function, are the values of x, for which f(x)=0


According to the "Rational Root Theorem", the rational roots of f, are factors of 60.

That is, when trying to find the roots of a polynomial function, it is a very good idea to first check the factors of the constant term.


All numbers shown in the choices are factors of 60, so we will solve the problem by trial:



`f(2)=2^4+6\cdot2^3-3\cdot2^2-52\cdot2-60=16+48-12-104-60 \\eq 0`

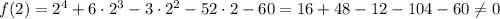
2 is not a root, so we eliminate choices A and D,

Choices B and C are almost equal, with only 1 different number, so let's check whether 5 is a root or not:



`f(5)=(5)^4+6\cdot(5)^3-3\cdot(5)^2-52\cdot(5)-60`


`=625+750-75-160-60=60`


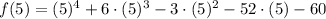
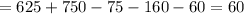
but


`f(-5)=(-5)^4+6\cdot(-5)^3-3\cdot(-5)^2-52\cdot(-5)-60`


`=625-750-75+160-60=0`

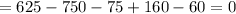
So the right choice is B