Question

How would the expression x^3+64 be rewritten using sum off cubes

Answer 1

`(x+4)(x^2-4x+4^2)`

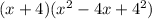
Explanation:

We have been given an expression
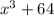`x^3+64` and we are asked to rewrite our expression using sum of cubes.

Sum of cubes:
`a^3+b^3=(a+b)(a^2-ab+b^2)`.

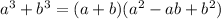We can rewrite 64 as:
`64=(4*4*4)=4^3`

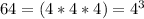
This means that a = x and b = 4, Upon substituting these values in sum of cubes formula we will get,

`x^3+64=(x+4)(x^2-4x+4^2)`

`x^3+64=(x+4)(x^2-4x+4^2)`

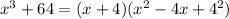
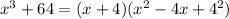
Therefore, after rewriting our given expression as sum of cubes we will get:
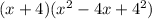`(x+4)(x^2-4x+4^2)`.

Answer 2

`\bf \textit{difference of cubes} \\ \quad \\ a^3+b^3 = (a+b)(a^2-ab+b^2)\qquad (a+b)(a^2-ab+b^2)= a^3+b^3 \\ \quad \\ a^3-b^3 = (a-b)(a^2+ab+b^2)\qquad (a-b)(a^2+ab+b^2)= a^3-b^3\\\\ -------------------------------\\\\ \boxed{64=4^3}\qquad x^3+64\implies x^3+4^3\implies (x+4)(x^2-x4+4^2) \\\\\\ (x+4)(x^2-4x+16)`