Question

The coordinates of the vertices of quadrilateral PQRS are P(−4, 2) , Q(3, 4) , R(5, 0) , and S(−3, −2).

Which statement correctly describes whether quadrilateral PQRS is a rectangle?

Quadrilateral PQRS is not a rectangle because it has only one right angle.

Quadrilateral PQRS is not a rectangle because it has only two right angles.

Quadrilateral PQRS is a rectangle because it has four right angles.

Quadrilateral PQRS is not a rectangle because it has no right angles.

Answer 1

Quadrilateral PQRS is not a rectangle because it has only one right angle.

Answer 2

Option A is correct.

As, Quadrilateral PQRS is not a rectangle because it has only one right angle.

Step-by-step explanation:

Given:

The coordinate of vertices of quadrilateral PQRS are P(−4,2), Q(3, 4), R(5,0) and S(−3,−2).

Slope for two points
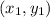`(x_(1),y_(1))` and
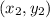`(x_(2),y_(2))` is given by:

`(y_(2)-y_(1))/(x_(2)-x_(1))`.

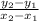The slope of PQ is
`(4-2)/(3-(-4)) =(2)/(7)`

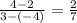
The slope of QR is
`(0-4)/(5-3) =(-4)/(2) = -2`

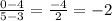
The slope of RS is
`(-2-0)/(-3-5) =(-2)/(-8) =(1)/(4)`

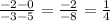
The slope of SP is
`(2-(-2))/(-4-(-3)) =(4)/(-1) =-4`

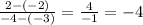
The slopes of perpendicular lines are opposite reciprocals.

∴ only one pair of sides has slopes that are negative reciprocals;

this means the figure has only 1 right angle, so it is not a rectangle.

Therefore, quadrilateral PQRS is not a rectangle because it has only one right angle.