Answer:
x=1, y=4
P=6
Explanation:
We are given that
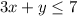
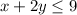
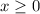
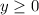
Objective function
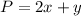
We have to values of x and y that maximize the P and maximum value of P .
First we change inequality equation into equality equation
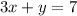 (I equation )
(I equation )
 (II equation)
(II equation)
Equation I multiply by 2 and then subtract from II equation
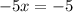
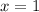
Substitute x=1 in equation I
Then, we get



The two equation intersect at point (1,4).
Substitute x=0 in equation I
Then , we get y=7
Substitute y=0 then
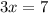
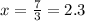
The equation I cut the x- axis at point (2.3,0)and y-axis at (0,7).
Substitute x=0 in equtaion II
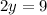
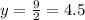
Substitute y=0
Then, we get
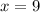
Therefore, the equation II cut the x- axis at point (9,0) and y axis at point (0,4.5).
Substitute x=0 and y=0 in inequality Equation I

It is true . Therefore, shaded region below the line.
Substitute x=0 and y=0 in inequality equation II
Then,
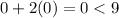
It is true. Therefore, the shaded region below the line.
The feasible region is bounded.The feasible region bounded by (0,0),(0,4.5),(2.3,0) and (1,4).
At (0,4.5)
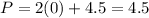
At (2.3,0)
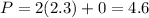
At (1,4)
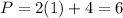
At (0,0)
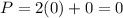
Hence, maximum value of P is 6 at (1,4).
x=1 and y=4