Question

Find the unknown sides and angles of each triangle using the laws of sines.

Answer 1

The law of sines states that:

`(A)/(\sin\alpha)=(B)/(\sin\beta)=(C)/(\sin \gamma)`

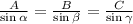
Where alpha is the opposite angle to the A-side, beta is the opposite angle to the B-side, and gamma is the opposite angle to the C-side.

In our case

`\begin{gathered} (12)/(\sin(80degree))=(8)/(\sin \theta) \\ \Rightarrow\sin \theta=(8\cdot\sin (80degree))/(12) \\ \Rightarrow\theta=\sin ^(-1)((8\cdot\sin(80degree))/(12)) \\ \Rightarrow\theta=\sin ^(-1)((2\cdot\sin (80degree))/(3)) \end{gathered}`

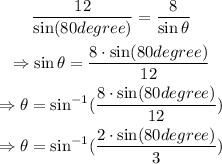
Then,

`\begin{gathered} \theta=41.04\text{degre}e \\ \Rightarrow\angle K=41.04degree \end{gathered}`

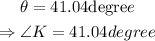
Thus, angle K is 41.04°

As for angle M, remember that the sum of the inner angles of a triangle is equal to 180°, therefore:

`\begin{gathered} \angle M=180-80-41.04=58.96 \\ \Rightarrow\angle M=58.96 \end{gathered}`

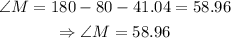
Then, angle M is equal to 58.96°.

Finally, as we know angle M, we can calculate the length of side m.

`\begin{gathered} (12)/(\sin(80degree))=(m)/(\sin (58.96degree)) \\ \Rightarrow m=(12)/(\sin(80degree))\cdot\sin (58.96degree)=10.44 \\ \Rightarrow m=10.44 \end{gathered}`

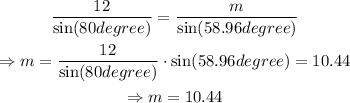
Then, m is equal to 10.44