Question

Given: r || s and q is a transversal

Prove: ∠4 is supplementary to ∠6


Given that r || s and q is a transversal, we know that
∠3 ≅ ∠6 by the .blank. Therefore, m∠3 = m∠6 by the definition of congruent. We also know that, by definition, ∠4 and ∠3 are a linear pair, so they are supplementary by the linear pair postulate. By the definition of supplementary angles, m∠4 + m∠3 = 180°. Using substitution, we can replace m∠3 with m∠6 to get m∠4 + m∠6 = 180°. Therefore, by the definition of supplementary angles, ∠4 is supplementary to ∠6.

Answer 1

Explanation:

Given: r || s and q is a transversal .

To Prove: ∠4 is supplementary to ∠6 .

Proof: It is given that r is parallel to s and q is a transversal, then

∠3 ≅ ∠6 by the (Alternate interior angles).

Therefore, m∠3 = m∠6 by the definition of congruency.

We also know that, by definition, ∠4 and ∠3 are a linear pair, so they are supplementary by the linear pair postulate.

By the definition of supplementary angles, m∠4 + m∠3 = 180°. (1)

Now, Using substitution,

We can replace m∠3 with m∠6 in equation (1) to get m∠4 + m∠6 = 180°. Therefore, by the definition of supplementary angles, ∠4 is supplementary to ∠6.

Hence proved.

Answer 2

Given:
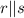`r || s` and q is a transversal.

Alternative Interior Angle states that a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal are equal.

By alternative interior angle;

`\angle 3 \cong \angle 6`

Definition of Congruent angles are angles that have the same degree of measurement.

Therefore,
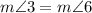`m\angle 3 = m\angle 6` [By definition of Congruent] .....[1]

Linear Pair states that a pair of adjacent angles formed when two lines are intersect.

therefore,
`\angle 4` and
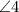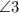`\angle 3` are a linear pair. [by definition of linear pair]

Two angles of linear pairs are always supplementary , which means their measure are add up to 180 degree.

By the definition of supplementary angles,
`m\angle 4 + m\angle 3 = 180^(\circ)` .....[2]

Substitute equation [1] in [2] we get,

`m\angle 4 +m\angle 6 =180^(\circ)`

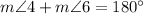
By the definition of supplementary angles,

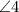`\angle 4` is supplementary to
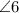`\angle 6` Hence proved!