Question

A country's population in 1991 was 48 million. In 2002 it was 51 million. estimate the population in 2008 using the exponential growth formula. Round to nearest million.

Answer 1

53 Million

Explanation:

In 1991: t = 0 and A = 45 million

In 2002: t = 11 and p = 51 Million

You're Solving For k:

P =
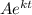`Ae^(kt)` In(1.0625) - In(
`e^(k*11)` )

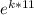51 =
`48^(k*11)` 0.0606 = k * 11

1.0625 =
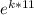`e^(k*11)` 0.0055 ≈ k

In 2008: t = 17

P =
`Ae^(kt)`

P =
`48e^(0.0055*17)`

P =
`48e^(0.094)`

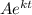
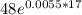
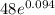
P = 48*1.0986

P ≈ 52.71466 million as the population

P ≈ 53 Million If Rounded

Answer 2

Using exponential growth, we get P1=P0*e^rt, where P1 is the result population, P0 is the initial population, r is the rate, and t is time. So:
51=48*e^11r
1.0625=e^11r
ln 1.0625=ln e^11r=11r ln e=11r
r=ln 1.0625/11=0.0055
Then
51*e^0.00551132925603953114369146654913*(2008-2002)=51*1.0336207977813425465939939376231=52.71466 million as the population
☺☺☺☺