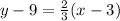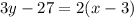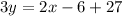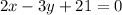Answer:
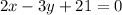
Explanation:
We are given that an equation

We have to find an equation of line which is perpendicular to given line and passing through the point (3,9).
We know that when two lines of slope
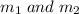 are perpendicular then
are perpendicular then
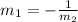
By comparing with

Where m=Slope of line
Slope of given line=
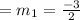
Slope of the line=
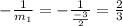
Slope of the line=

The equation of line passing through the point (3,9) is given by

Substitute the values
The equation of line which passing through the point (3,9) is given by