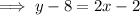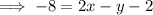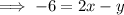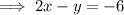Answer:

Explanation:

Rewrite the given equation in slope-intercept form by isolating y:
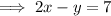
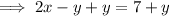
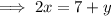
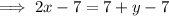
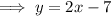
Therefore, the slope of the given equation is 2.
If two lines are parallel, their slopes are the same.
Therefore, the slope of the line parallel to the given line is 2.

Substitute the found slope 2 and the given point (1, 8) into the point-slope formula:
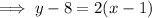
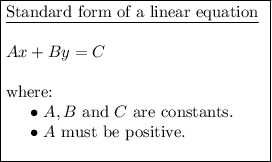
Expand the found equation and rewrite it in standard form: