Solution:
Given:
The table of the poll results;
The formula for calculating probability is given by;
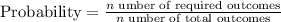
a) The P(Democrat) is;

Therefore, the probability that it is a democrat is 0.3625
b) The P(worse) is;
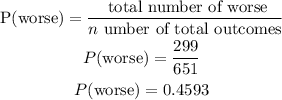
Therefore, the probability that it is worse is 0.4593
c) The P(worse|Democrat)- This is a conditional probability.
We use the conditional probability formula to solve this.
Conditional probability is given by;
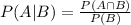
Hence,

Therefore, the probability of worse given democrat is 0.5805
d) The P(Democrat|worse) is;

Therefore, the probability of democrat given worse is 0.4582
e) The P(Democrat and worse) is;

Therefore, the probability of democrat and worse is 0.2105