Question

myopenmath.comA CBS News poll involved a nationwide random sample of 651 adults, asked those adults about theirparty affiliation (Democrat, Republican or none) and their opinion of how the US economy waschanging ("getting better," "getting worse" or "about the same"). The results are shown in the tablebelow.betterworsesame1043844RepublicanDemocrat128790137118none21If we randomly select one of the adults who participated in this study, compute the followingprobabilities. (round to four decimal places)a. P (Democrat) =b. P (worse) =C. P (worse Democrat) =d. P (Democrat worse) =e. P(Democrat and worse) =CalculatorScratchwork Area

Answer 1

Given:

The table of the poll results;

The formula for calculating probability is given by;

`\text{Probability}=\frac{n\text{ umber of required outcomes}}{n\text{ umber of total outcomes}}`

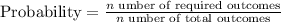
a) The P(Democrat) is;

`\begin{gathered} \text{P(Democrat)}=\frac{\text{ total number of democrat}}{n\text{ umber of total outcomes}} \\ P(\text{Democrat)}=(236)/(651) \\ P(\text{Democrat)}=0.3625 \end{gathered}`

Therefore, the probability that it is a democrat is 0.3625

b) The P(worse) is;

`\begin{gathered} \text{P(worse)}=\frac{\text{ total number of worse}}{n\text{ umber of total outcomes}} \\ P(\text{worse)}=(299)/(651) \\ P(\text{worse)}=0.4593 \end{gathered}`

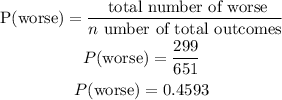
Therefore, the probability that it is worse is 0.4593

c) The P(worse|Democrat)- This is a conditional probability.

We use the conditional probability formula to solve this.

Conditional probability is given by;

`P(A|B)=(P(A\cap B))/(P(B))`

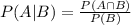
Hence,

`\begin{gathered} \text{Probability of worse given democrat=}\frac{P(worse\text{ and democrat)}}{\text{Probability (democrat)}} \\ P(\text{worse}|\text{democrat)}=(137)/(651)\text{ /}(236)/(651) \\ P(\text{worse}|\text{democrat)}=(137)/(651)*(651)/(236) \\ P(\text{worse}|\text{democrat)}=(137)/(236) \\ P(\text{worse}|\text{democrat)}=0.5805 \end{gathered}`

Therefore, the probability of worse given democrat is 0.5805

d) The P(Democrat|worse) is;

`\begin{gathered} \text{Probability of democrat given worse=}\frac{P(democrat\text{ and worse)}}{\text{Probability (worse)}} \\ P(\text{democrat}|\text{worse)}=(137)/(651)\text{ /}(299)/(651) \\ P(\text{democrat}|\text{worse)}=(137)/(651)*(651)/(299) \\ P(\text{democrat}|\text{worse)}=(137)/(299) \\ P(\text{democrat}|\text{worse)}=0.4582 \end{gathered}`

Therefore, the probability of democrat given worse is 0.4582

e) The P(Democrat and worse) is;

`\begin{gathered} P(A|B)=(P(A\cap B))/(P(B)) \\ P(A\cap B)=P(A|B)* P(B) \\ P(\textworse)* P(worse) \\ P(\text{Democrat}|\text{worse) calculated in option (d) above = 0.4582} \\ P(\text{worse) calculated in option (b) above = 0.4593} \\ \\ \text{Hence,} \\ P(\textworse)* P(worse) \\ P(\text{Democrat and worse)=}0.4582*0.4593 \\ P(\text{Democrat and worse)=}0.2105 \\ \\ \\ \\ \text{Alternatively,} \\ P(\text{Democrat and worse)=}\frac{n\text{ umber of democrat and worse}}{\text{total number}} \\ P(\text{Democrat and worse)=}(137)/(651) \\ P(\text{Democrat and worse)=}0.210445 \\ P(\text{Democrat and worse)=}0.2105 \end{gathered}`

Therefore, the probability of democrat and worse is 0.2105