Question

Find the sum of the following infinite geometric series, if it exists. ½ + -¼ + ⅛ + -1/16 +...

Answer 1

hmm

each term is multiplied by a constant
1/2 times what=-1/4? that is -1/2
-1/4 times what=1/8? that is -1/2

so r=-1/2

does it converge or diverge?
if it converges, it has an infinite sum
if it diverges, it does not

if |r|<1 then it converges
|-1/2|<1?
1/2<1?
true
it converges and has a sum

the sum of an infinite geometric series is

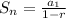
`S_n=(a_1)/(1-r)` where a1 is the first term and r=common ratio

a1=1/2
r=-1/2


`S_(\infty)=((1)/(2))/(1-((-1)/(2)))`

`S_(\infty)=((1)/(2))/(1+(1)/(2))`

`S_(\infty)=((1)/(2))/((3)/(2))`

`S_(\infty)=((1)/(2))((2)/(3))`

`S_(\infty)=(2)/(6)`

`S_(\infty)=(1)/(3)`



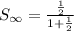
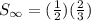
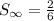
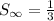
the sum is
`(1)/(3)`