Question

How to express volume of a cube as a monomial

Answer 1

`V=27c^(18)d^(6)\ units^3`

Explanation:

The complete question in the attached figure

we know that

The volume of a cube is equal to

`V=b^3`

where b is the length side of a cube

In this problem we have

`b=3c^(6)d^(2)`

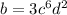
substitute in the formula

`V=(3c^(6)d^(2))^3`

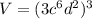
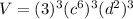`V=(3)^(3)(c^(6))^(3)(d^(2))^(3)` -----> by power of a product

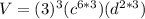`V=(3)^(3)(c^(6*3))(d^(2*3))` ----> by power of a power

Simplify

`V=27c^(18)d^(6)\ units^3`