Question

Israel started to solve a radical equation in this way: Square root of x plus 6 − 4 = x Square root of x plus 6 − 4 + 4 = x + 4 Square root of x plus 6 = x + 4 (Square root of x plus 6)2 = (x + 4)2 x + 6 = x2 + 8x + 16 x + 6 − 6 = x2 + 8x + 16 − 6 x = x2 + 8x + 10 x − x = x2 + 8x + 10 − x 0 = x2 + 7x + 10 0 = (x + 2)(x + 5) x + 2 = 0 x + 5 = 0 x + 2 − 2 = 0 − 2 x + 5 − 5 = 0 − 5 x = −2 x = −5 Solutions = −2, −5 What error did Israel make?

Answer 1

The correct procedure is

`√(x+6) -4=x \\ √(x+6) =x+4 \\ x+6=(x+4)^(2) \\x+6=x^(2)+8x+16 \\0=x^(2)+7x+10`

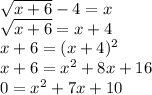
This quadratic equation factorizes into
(x + 5)(x + 2) = 0
x = -5 or x = -2.

It is customary to plug the two solutions back into the original equation in order to reject extraneous solutions.
When x = -5,
√(x+6) = 1
x+4 = 1
Accept this solution.

When x = -2,
√(x+6) = 2
x+4 = 2
Accept this solution.

Answer:
Israel solved the problem correctly by obtaining x = -2, -5, but he did not check for extraneous solutions