Question

Can a sequence be both arithmetic and geometric?

Answer 1

an aritmetic sequence is like this

`a_n=a_1+d(n-1)` where a1=first term and d=common difference

geometric is
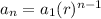
`a_n=a_1(r)^(n-1)` where a1=first term and r=common ratio


can it be both aritmetic and geometric
hmm, that means that the starting terms should be the same

therfor we need to solve
`d(n-1)=(r)^(n-1)`
what values of d and r make all natural numbers of n true?
are there values that make all natural numbers for n true?

when n=1, then d(1-1)=0 and r^(1-1)=1, so already they are not equal

the answer is no, a sequence cannot be both aritmetic and geometric