Question

A spring whose natural length is 1010 cm exerts a force of 3030 n when stretched to a length of 1515 cm. (note 1515 cm - 1010 cm = 55 cm = .05.05 m ) find the spring constant k=k= 2 determine the work done in stretching the spring 77 cm ( =.07=.07 m) beyond its natural length. w=w= joules

Answer 1

The equation that relates the spring extension to the force applied to it is linear:

`F=k*\Delta x`
where
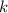
`k` is the spring constant.
Hence
`k= (F)/(\Delta x)= (3030)/((15.15-10.10))= (3030)/(5.05)=600 ( (N)/(m) )`
because
`1 m = 100 cm`
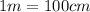
The work done when stretching the spring is

`W= -\int\limits^d_0 {F(x)} \, dx= -\int\limits^d_0 {(kx)} \, dx = -(kx^2)/(2)= (600*0.77^2)/(2)= -177.87 (Joules)`
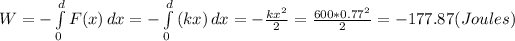
The work is negative because we stretch the spring while the string oposes to this stretching.