Question

What is the wavelength (angstroms) of a photon that has an energy of 5.69 × 10-17 j?

Answer 1

Answer: The correct answer is
`\lambda= 35\AA`.

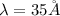Step-by-step explanation:

The expression for the relation between the energy of the wave and the wavelength is as follows;

`E=(hc)/(\lambda )`

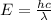
Here, E is the energy of the wave, h is Planck's constant, c is the speed of the light and
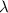`\lambda` is the wavelength of the wave.

It is given in the problem that the energy of the photon is
`5.86* 10^(-17) J`.

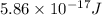Put c=
`3* 10^(8) meter per second`,
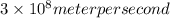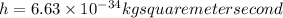`h=6.63* 10^(-34) kg square meter second` and

`5.69* 10^(-17)=((6.63* 10^(-34))(3* 10^(8)))/(\lambda )`

`\lambda= 3.5* 10^(-9)`

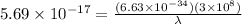
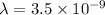
Convert the value of the wavelength into angstrom.

`1 \AA = 10^(-10) m`

`\lambda= (3.5* 10^(-9)m)/(10^(-10)\AA )`

`\lambda= 35\AA`

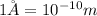
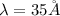
Therefore, the wavelength of a photon is
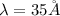`\lambda= 35\AA`.

Answer 2

E = hc / λ

Rearranging to get the wavelength (lambda):
λ = hc / E
λ = 6.63x10^-34 Js x 3.00x10^8 m/s / 5.69x10^-17J
λ = 3.50x10^-9 m

3.5x10^-9 m x (100 cm / 1 m) x (1x10^8 Å / 1 cm) = 35 Å