Question

Tank A initially contained 124 liters of water. It is then filled with more water, at a constant rate of 9 liters per minute. How many liters of water are in Tank A after 80 seconds have passed? How many liters of water are in Tank A after x minutes have passed (answer should be an expression and not an equation)?

Answer 1

Given the information, we can model the capacity of Tank A with the following relation function:

`y=124+9x`

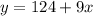
where 'y' are the liters inside the tank and x is the minutes that pass.

To find out how many liters of water are n Tank A after 80 seconds, first we must covert 80 seconds to minutes:

`80\sec =(80)/(60)\min =(8)/(6)\min =(4)/(3)min`

then, doing x=4/3, we get:

`\begin{gathered} x=(4)/(3) \\ \Rightarrow y=124+9((4)/(3))=124+(3\cdot4)=124+12=136 \\ y=136 \end{gathered}`

therefore, after 80 seconds, there are 136 liters in Tank A.

The expression fo know how many liter