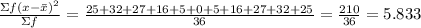Question

A: Find the mean and standard deviation of the sums you should get when you roll two standard number cubes

B: Suppose you can replace one number cube with a nonstandard number cube, where any of the numbers 1 through 6 can appear on multiple faces. How can you arrange the numbers on the nonstandard cube so that the mean of the rolls is the same as that of two standard number cubes, but the standard deviation is as large as possible? What is this value? Explain your thinking.

Answer 1

The table showing the sums and the number of appearance is given below:

sum(x) number of appearance(f) x - x(bar) (x - x(bar))^2 f(x - x(bar))^2
2 1 -5 25 25
3 2 -4 16 32
4 3 -3 9 27
5 4 -2 4 16
6 5 -1 1 5
7 6 0 0 0
8 5 1 1 5
9 4 2 4 16
10 3 3 9 27
11 2 4 16 32
12 1 5 25 25

Mean is given by

`(\Sigma fx)/(\Sigma f) = (2*1+3*2+4*3+5*4+6*5+7*6+8*5+9*4+10*3+11*2+12*1)/(1+2+3+4+5+6+5+4+3+2+1) \\ \\ = (2+6+12+20+30+42+40+36+30+22+12)/(36) = (252)/(36) =7`

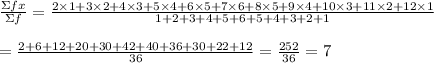
The standard deviation is given by:

`\frac{\Sigma f(x-\bar{x})^2}{\Sigma f} = (25+32+27+16+5+0+5+16+27+32+25)/(36) = (210)/(36) =5.833`