Question

Suppose that the scores on a reading ability test are normally distributed with a mean of 60 and a standard deviation of 8. What proportion of individuals score more than 55 points on this test? Round your answer to at least four decimal places.

Answer 1

The z-score can be found the following formula:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ \text{where }\mu\text{ is the mean and }\sigma\text{ is the standard deviation} \end{gathered}`

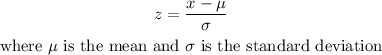
x is the value we want to find the z-score, we need to do this first as follows:

`\begin{gathered} z=(55-60)/(8) \\ z=(-5)/(8) \\ z=-\text{0}.625 \end{gathered}`

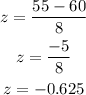
Thus, the find the proportion of individuals that score more than 55 points, we need to find the probability of z>-0.625. It can be written as:

`P(z>-0.625)=1-P(z\le-0.625)`

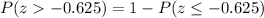
In a standard normal table, we can search the probability of z<=-0.625, it is:

0.26599.

By replacing this value in the formula we obtain:

`\begin{gathered} P(z>-0.625)=1-0.26599 \\ P(z>-0.625)=0.7340 \end{gathered}`

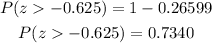
The proportion of individuals that score more than 55 points on this test is 73.4% of the total number of individuals.