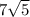Question

Line stack A B with bar on top is partitioned at point C, with ratio 3:4, and its midpoint is D.

A(6,17)

B(13,3)

Coordinates for point C    , point D (decimal)

Distance for stack AB with bar on top (in radical form)

Answer 1

easy

ok, so the midpoint formula
the midpoint of the 2 points
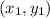
`(x_1,y_1)` and
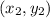
`(x_2,y_2)` is

`((x_1+x_2)/(2),(y_1+y_2)/(2))`
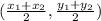
so midpoint of (6,17) and (13,3) is

`((6+13)/(2),(17+3)/(2))`=

`((18)/(2),(20)/(2))`=
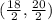
(9,10)

point D is (9,10)


ok, so the other onne

this is kind of tricky but not

we must do
3:4 right?
so 3+4=7
divide the line into 7 segments and take 3 of them
Assming AC:CB=3:4
hmm, to divide the segment into 1:1, we did 1+1=2, and multiplied each sum of points by 1/2
so multiply each by 3/7


`((3(6+13))/(7),(3(17+3))/(7))`

`((3(18))/(7),(3(20))/(7))`

`((54)/(7),(60)/(7)`
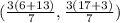
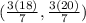
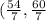
in decimal
(7.7142857142857142857142857142857,8.5714285714285714285714285714286)


distance between (x1,y1) and (x2,y2) is

`D=√((x_1-x_2)^2+(y_1-y_2)^2)`
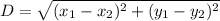
distance between (6,17) and (13,3) is

`D=√((6-13)^2+(17-3)^2)=`

`D=√((-7)^2+(14)^2)=`

`D=√(49+196)=`

`D=√(245)` =
`7√(5)`





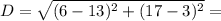
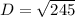
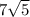
point C is
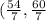
`((54)/(7),(60)/(7)` or (7.7142857142857142857142857142857,8.5714285714285714285714285714286) in decimal
point D is (9,10)
Distance between points A and B is
`√(254)` or
`7√(5)`