As per the question the height of object
![[h_(0) ]](https://img.qammunity.org/2018/formulas/physics/middle-school/ubv607r7luz8ob23n45zmp0z7uk2dcnex3.png) 18 mm
18 mm
The object distance [u] is given as 12 mm
The image distance[v] is given as 4 mm
The lens taken here is a diverging nature.hence the lens is a concave lens.
The image formed in a concave lens is always virtual,erect and diminished.
As per the question the image is formed in front of the lens.
we have to calculate the image height
![[h_(i) ]](https://img.qammunity.org/2018/formulas/physics/middle-school/47k5t6gjd9vm32z7ys6ay08sg9nc99kd8f.png) which is calculated as follows-
which is calculated as follows-
putting the sign convention on the above data we get
u= -12 mm v=-- -4 mm [ - sign is due to the fact that the measurement is opposite to the direction of light
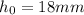 [the height is positive as it is above the principal axis]
[the height is positive as it is above the principal axis]
As per the magnification formula we know that
Magnification
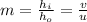
⇒
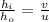
⇒
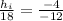
⇒
![h_(i) =(18*[-4])/([-12])](https://img.qammunity.org/2018/formulas/physics/middle-school/ks2sriovhgzfad6q7m11pfqdx5nt5hijny.png)
= 6 mm [ans]
Hence B is right.