Question

Find the first, fourth, and tenth terms of the arithmetic sequence described by the given rule.

A(n) = –3 + (n – 1)(–2.2)

Answer 1

An arithmetic sequence with first term a, and a common distance d si as follows:

m, m+d, m+2d, m+3d, ...

(for example: 3, 8, 13, 18 .... m=3, d=5)


let
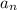
`\displaystyle{ a_n` be the n'th term of the arithmeti sequence

m, m+d, m+2d, m+3d, ...


then


`a_1=m\\\\a_2=m+d\\\\a_3=m+2d\\\\a_4=m+3d \\\\ .\\\\.`

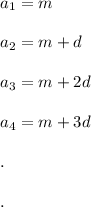
so it is clear that the n'th term, si given by :


`a(n)=m+(n-1)d`


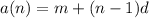
compare the rule we found with the given rule A(n)=-3+(n-1)(-2.2)

it is clear that m=-3, and d=-2.2,

so the sequence

m, m+d, m+2d, m+3d, ...

becomes:

-3, -3-2.2, -3-2*2.2, -3-3*2.2, ....

so

-3, -5.2, -7.4, -9.6


the first term is -3, the fourth term is -9.6, the 10th term can be found by plugging in n=10 in the formula:


A(10) = –3 + (10 – 1)(–2.2)=-3+9(-2.2)=-3-19.8=-22.8




remark, we could have use the formula directly and solve for A(1), A(4) and A(10),

but with the explanations we see how we find derive the formula, and makes it easier to derive, even when we don't remember it properly.



Answer:

1st term=-3

2nd term=-9.6

10th term = -22.8