Question

In a classic carnival ride, patrons stand against the wall in a cylindrically shaped room. Once the room gets spinning fast enough, the floor drops from the bottom of the room! Friction between the walls of the room and the people on the ride make them the “stick” to the wall so they do not slide down. In one ride, the radius of the cylindrical room is R=7.5m and the room spins with a frequency of 20 revolution per minute.1) what is the normal force of the wall on a rider of m=50kg.2) what is the minimum coefficient of friction needed between the wall and the person?3) if a new person with mass 100kg rides the ride, what minimum coefficient of friction between the wall and the person would be needed?4) To be safe, the engineers making the ride want to be sure the normal force does not exceed 2.3 times each persons weight-and therefore adjust the frequency of revolution accordingly. What is the minimum coefficient of friction now needed?

Answer 1

1) 1644.93 N

2) 0.29

3) 0.29

4) 0.43

Step-by-step explanation:

We can represent the force acting on a person as follows:

So, we have the friction force which should be equal to the weight to keep the person in the same position, and we have the Normal force which in this case is equal to the centripetal force.

Using the radius r = 7.5 m and the frequency f = 20 rev per minute.

We can calculate the linear velocity and the centripetal acceleration as:

`\begin{gathered} v=2\pi fr=2\pi((20rev)/(\min ))(7.5m)=942.48\text{ m/min} \\ v=942\text{ m/min }*\frac{1\text{ min}}{60\text{ sec}}=15.71\text{ m/s} \end{gathered}`
`a_c=\frac{v^2_{}}{r}=(15.71^2)/(7.5)=32.89m/s^2`

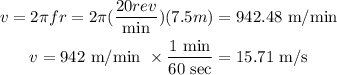
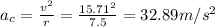
Therefore, the Normal force on a rider of 50 kg, will be

Then, taking into account the vertical forces and that Ff = μN, we can find the minimum coefficient of friction μ as follows:

`\begin{gathered} F_f=W \\ \mu N=mg \\ \mu=(mg)/(N) \\ _{}\mu=(50(9.8))/(1644.93)=0.29 \\ \end{gathered}`

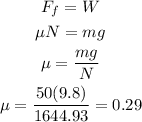
If a new person with a mass of 100kg rides the ride, the normal force will be equal to:

N = ma = 100kg(32.89) = 3289 N

Then, the coefficient of friction will be:

`\mu=(mg)/(N)=(100(9.8))/(3289)=0.29`

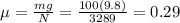
Finally, if the normal force doesn't exceed 2.3 times each person weight, them:

N = 2.3mg

So, the minimum coefficient of friction will be:

`\mu=(mg)/(N)=(mg)/(2.3mg)=(1)/(2.3)=0.43`

Therefore, the answers are:

1) 1644.93 N

2) 0.29

3) 0.29

4) 0.43